如何搞定机器学习中的拉格朗日？看看这个乘子法与KKT条件大招-电子技术方案|电路图讲解

一 前置知识 拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法，通过引入拉格朗日乘子，可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题。在介绍拉格朗日乘子法之前，先简要的介绍一些前置知识,然后就拉格朗日乘子法谈一下自己的理解。  

1.梯度 梯度是一个与方向导数有关的概念，它是一个向量。在二元函数的情形，设函数f(x,y)在平面区域D内具有一阶连续偏导，则对于每一点P(x0,y0)∈D，都可以定义出一个向量:fx(x0,y0)i+fy(x0,y0)j ,称该向量为函数f(x,y)在点P(x0,y0) 的梯度。并记作grad f(x0,y0) 或者∇f(x0,y0),即 grad f(x0,y0) = ∇f(x0,y0) = fx(x0,y0)i+fy(x0,y0)j=(fx(x0,y0),fy(x0,y0)) 。   再来看看梯度和方向导数的关系：如果函数f(x,y)在P(x0,y0)点可微，el = (cosα,cosβ)是与方向L同向的单位向量，则∂f/∂L|(x0,y0) = fx(x0,y0)cosα+fy(x0,y0)cosβ = grad f(x0,y0).el =  |grad f(x0,y0)|.cosθ ，其中θ表示的梯度与el 的夹角。由此可知，当θ = 0时,el 与梯度的方向相同时，此时方向导数最大，函数f(x,y)增长最快;当θ = π时,el 与梯度的方向相反时，此时方向导数最小且为负,函数f(x,y)减小最快。  

2.等高线(等值线) 通常来说，二元函数 z = f(x,y)在几何上表示一个曲面，这个曲面被平面 z = c(c为常数)所截得的曲线L的方程为:   　　　　　　　　　　　　　　　　　　　　　　　　　　　        　 这是一条空间曲线，这条曲线L在xOy平面上的投影是一条平面曲线L*，它在xOy平面直角坐标系中的方程为：f(x,y) = c .对于曲线L*上的一切点，已给函数的函数值都是c，所以我们称平面曲线L*为函数z = f(x,y)的等值线(等高线)。再来看看等高线的一些性质：   若fx，fy不同时为零，则等高线 f(x,y) = c上任一点P(x0,y0)处的一个单位法向量为: 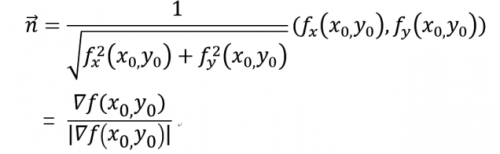  这表明函数f(x,y)在一点(x0,y0)的梯度∇f(x0,y0)的方向就是等高线f(x,y) = c在这点的法向量的方向，而梯度的模|∇f(x0,y0)|就是沿这个法线方向的方向导数∂f/∂n,于是有：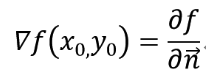                                            

。 （本文来源网络整理，目的是传播有用的信息和知识，如有侵权，可联系管理员删除）