第二部分:带有热敏电阻器SPICE模型的PID控制器可实现精确的温度曲线控制
Alain Stas现任Vishay非线性电阻器产品营销工程师,此前曾在布鲁塞尔自由大学(ULB)研究生物化学过程的数学建模。Alain拥有布鲁塞尔自由大学土木工程物理学硕士学位,专业是固态电子学。 引言 现如今,使用软件(如Simulink MATLAB)来构建温度控制系统已变得相对简单。根据这些系统的复杂程度,可用PI、PID或模糊逻辑控制器进行温度调节。但使用简单并不一定意味着低成本,因为这些软件可能非常昂贵。对基于NTC热敏电阻器的温度控制应用,可达到的精度主要取决于热敏电阻器的特征(包括容差)鉴定方法。
本文的焦点不是Simulink,而是在简单系统中实现良好温度调节的零成本DIY方法。这将在高性能LTSpice电子仿真器和先前描述的精密热敏电阻器模型的帮助下进行。 我们可以看到用一个SPICE模型来表示一个简单系统的温度,并将该温度反馈给用于控制系统温度的电压驱动热敏电阻器是可以实现的。现在我们利用基于NTC热敏电阻器(完全模拟式)的PID控制器及其LTSpice模型进入到调节的下一个层级。该PID控制器的目的是用已定义的曲线来控制一个系统(如小炉子)的温度。仿真的目的是尽可能接近所定义的曲线,并保持最小温度偏差。对于该应用,炉温必须在稍长于一小时的时间内进行如下变化。
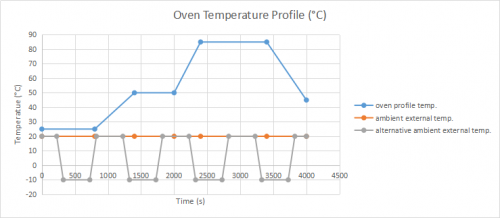
图1 该温度曲线是我们需要PID控制器的主要原因之一,它将能非常准确地遵循所要求的停延和斜坡(dwell and slope),同时尽可能避免大振荡。我们PID控制器的第二个任务是使系统能够对外部热/冷噪声做出反应,例如图1中的替代曲线(灰色曲线)描述的外部温度变化。因此我们将详细说明电路建议,对其进行仿真和优化,并提供一些关于如何将该理论工作与实际测量联系起来的提示。
仿真描述总电路如图2所示,附带如下说明: ?感测桥中有两个NTCLE203E3103_B0热敏电阻器。一个是物理感测电阻器:感测系统温度的温度传感器,具有时间延迟(等于连接到节点Ti的网络的RC常数)。第二个热敏电阻器仅用于仿真。在Tset节点连接一个分段线性文件电压。该文件包含关于所采用温度曲线的临时信息(见图1的定义)。这是对我们的参考曲线进行编程的理想方式。 ?加热器单元由两个固定电阻器R8和R9与一个基于两个ZTXB49 NPN晶体管的达林顿装置组成。 ? “系统”的右边是炉子的粗略示意图,电容器Csystem代表其热质量。炉子产生的热通过B4 ABM(模拟行为)电压源进行模拟,其中包括从炉子向周围温度Tamb的发散。 ?增加一个串联脉冲源(热噪声,本例中是一个冷源),以充分代表外部环境温度的变化(参数中幅度为dT的脉冲)。
?SPICE指令包含PID参数Kp、Kd和Ki;寄生环境源dT;热敏电阻器响应时间Tau;固定电阻器容差RTOL;以及NTC热敏电阻器容差Rntctol和针对B25/85系数的BTOL。另外还用两个特殊函数vb()和wc() [3]来对最坏的情况做分析。 ?Err函数是所生成的系统温度Tsystem与设定温度Tset之差的LTSpice RMS函数。该err函数必须在仿真时间内全局最小化,并对所有电路参数提供最佳的值。
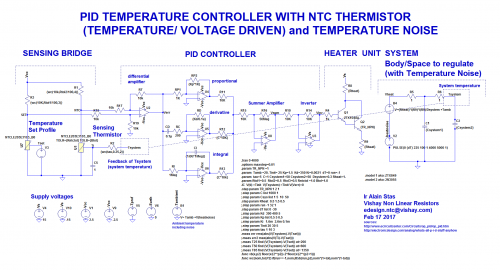
图2 仿真结果 在此电路的帮助下,我们进行了不同的仿真,以便继续参数优化。我们需要找到Kp、Kd和Ki的值,使得err函数是最小的。LTSpice允许您每次模拟最多扫描三个参数,所以您甚至能够在一次运行(虽然时间非常长)中优化Kp、Kd和Ki。当然,这里我们只介绍优化的一个步骤及最终结果。 在图3中,仿真在下方窗格中显示了V(Tsystem) 和目标V(Tset) 的结果,在上方窗格中显示了电压 / 温度的差。在图2的SPICE指令中,我们要求测量err函数,它是仿真的整个时间范围上结果与目标值之差的和的最小二乘方。该err结果写在可从LTSpice的“View”菜单获得的“SPICE Error Log”文件中。 图3中显示了Ki的优化步骤,其中Ki是在1.6 m和2.6 m距离扫描得到。 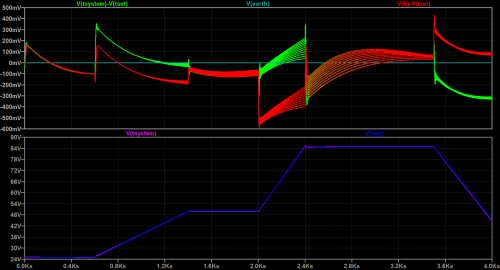
图3 最小二乘方err函数可在图2中的仿真完成后在Ki值的函数中读取。SPICE Error Log文件数据的图形表示将在图4中显示最佳Ki值(Kp = 2.1 m)。
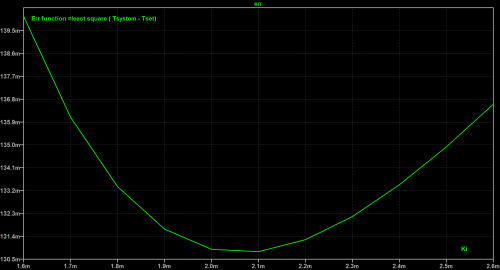
图4 同时,我们需要针对预先选择的两个NPN晶体管来优化Rheat值,并使我们的调节在环境温度变化时仍然稳定。这就是图5中进行的仿真。在下方窗格中,我们看到两条环境温度迹线(一个恒定于20 °C,另一个在20 °C 至 -10 °C范围内摆动(因此dT为-30 °C))。在上方窗格中,我们看到这些环境变化几乎被加热电流的增加抵消,以便使系统温度尽可能接近设定温度。
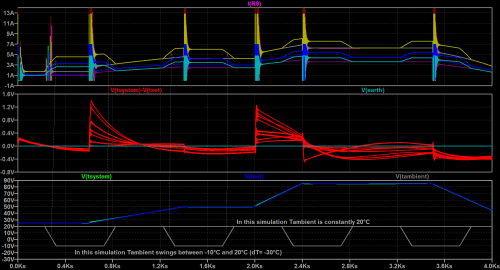
图5 通过查看SPICE Error Log文件再次计算err函数(图6),我们得到Rheat的优化值1.5 ,无论是什么晶体管模型。 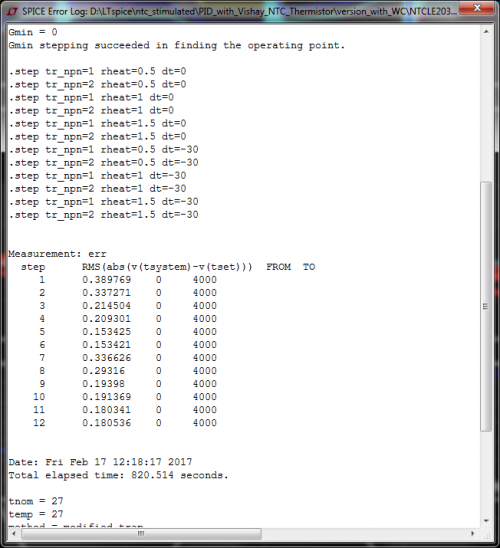
图6 当所有参数优化完毕后,我们再次继续仿真,并获得最终结果(图7)。
。 (本文来源网络整理,目的是传播有用的信息和知识,如有侵权,可联系管理员删除)
版权声明:网站转载的所有的文章、图片、音频视频文件等资料的版权归版权所有人所有。如果本网所选内容的文章作者及编辑认为其作品不宜公开自由传播,或不应无偿使用,请及时联络我们,采取适当措施,避免给双方造成不必要的经济损失。